AVL树原理详解及实现
1 几个重要的概念
- 从结点$n_{1}$到$n_{k}$的路径(path):从结点$n_{1}$到$n_{k}$,沿树经历的所有的结点构成的序列;
- 路径长度(length):路径上的边的个数(注意不是结点个数),从$n_{1}$到$n_{k}$,路径长度也就是$k-1$;也就是说,每个结点到它自身的路径长度为0;
- 结点$n_{i}$深度:从根节点到$n_{i}$的路径长度。比如根结点的深度为0;
- 结点$n_{i}$高度:从$n_{i}$到所有叶子结点的路径中的最长路径长度。因此叶子结点的高度都为0。树的高度就是根节点的高度;
- 树的深度是其中最深的叶子结点的深度 = 树的高度;
2 普通二叉搜索树的缺陷
对于普通的二叉搜索树,当我们从小到大插入1到10时,因为每次都插在树的最右节点上,因此树的高度和插入的结点个数相同。那么对该树的操作,最大的时间复杂度为O(n),最小为O(1)。因此,对于普通的搜索二叉树,一个特性是树的高度和插入的结点的大小顺序紧密相关,因此极易出现树的子树高度不均衡的情况。对树的操作又和结点的位置息息相关,因此可能出现部分操作时间复杂度较大(为O(n))的情况。
我们希望充分利用树的二叉结构,让树的高度差不多为logN,这样操作的时间复杂度也为O(logN)。我们无法让每颗左右子树高度相同,这样对二叉搜索树的要求太苛刻。但是我们可以让左右子树的高度差别不大于1,这就提出了平衡二叉树(AVL树)的概念。我们首先探究一下平衡二叉树的结点个数及结构,和不平衡的情况,然后引入本文的重点:平衡二叉树的实现。
3 平衡树的结点个数及结构
AVL树的左右子树深度差别不大于1。设左右子树的高度差为左子树的高度减去右子树的高度,那么高度差的结果只能为1,-1和0(根据定义,空树的高度为-1,仅有1个根节点的树的高度为0)。
下面我们探究一下高度为$h$的平衡二叉树的最小结点个数。假设平衡树的高度为9,那么其左右子树的高度最多为8,又因为我们想要实现节点个数最少,而左右子树的高度可以相差1,因此设左子树的高度为7,右子树的高度为8。
由此我们可以得出一个公式,$S(h) = S(h-1) + S(h-2) + 1$,其中$S(-1) = 0, S(0) = 1$。这里的$S(h)$指的是高度为$h$的平衡二叉树的最少结点个数。根据前文,对于高度为$h$的平衡二叉树,其左右子树的高度最大为$h-1$,而因为左右子树高度可以相差1,要想让节点的个数最少,左子树的高度为$h-1$,右子树的高度为$h-2$,因此左右子树的最少节点个数分别为$S(h-1)$和$S(h-2)$,那么加上根节点,高度为$h$的平衡二叉树的总的最少节点个数为$S(h-1)+S(h-2)+1$。我们其实可以发现,这个结构有点类似于斐波那契数列$S(h) = S(h-1) + S(h-2)$ ,其中$S(-1) = S(0) = 1$。
而这里我们想要通用的分析一下一个高度为$h$的平衡二叉树的结构。如果是满二叉树,那么其节点的个数为$2^{h+1}-1$,而最小的结点个数为$S(h-1) + S(h-2) + 1$。我们列举一些基础的$h$的情况:
| 高度$h$ | 最小结点个数 | 最大结点个数 |
|---|---|---|
| -1 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 2 | 3 |
| 2 | 3 | 7 |
| 3 | 6 | 15 |
可以看到的是,随着$h$增大,平衡术的最小结点个数和最大结点个数的差异逐渐增大。此外,平衡树的结构是不一定的,它并不是从上一层到下一层,一层层的按顺序插入/删除结点,因此如果按照高度来对平衡树的结构和不平衡树的情况来进行讨论,是不合理的。因此,我们在后文主要通过对几种出现不平衡树的情况进行分类讨论,对每种讨论建立对应的处理方式,来保证树的平衡化。
4 不平衡的情况分析
要探究平衡二叉树操作后不平衡的情况,需要满足如下两点:
- 在操作(插入或删除)之前,二叉树是平衡的:也就是说,在操作之前,该平衡树中的所有子树都都满足左右子树高度差不大于1;
- 在操作之后,二叉树不平衡了:也就是说,在插入了一个结点之后,以某个结点为根的二叉树不是平衡树了。
需要注意的是,插入或删除以后不一定导致所有的祖先树都失去平衡。比如根节点的左子树比右子树的高度少1,但是左右子树都是平衡树。插入一个结点后,可能由于结构原因,导致这个左子树不再是平衡树,但是树的高度加了1,那么现在根节点的左子树和右子树的高度差别为0了。因此虽然某棵子树不是平衡树了,但是在根节点处依然是平衡的。删除操作同理。因此,我们仅仅需要分析出现不平衡的情况的结点,以及及其为根的树,而不是处理整棵树。
我们设左右子树的高度差为D,其中D为左子树高度减去右子树高度。其中D的取值仅有三种:1,0和-1。我们不必细致的考虑左右子树中到底有几个结点,左右子树分别长什么样子,是什么结构,这样的情况是很多的,是分析不完的。我们只需要分析一个抽象的结构,知道是树中的哪个部分导致了不平衡的情况发生就行。
4.1 插入情况分析
首先,我们要思考一下,这棵树中至少有几个结点,才会满足:插入结点前的树是平衡树,而插入节点后的树不再是平衡树了。
这棵树可能是空树吗?当然不行,空树插入节点后,那也只有1个结点,还是棵平衡树。
这棵树可能只有1个结点吗?也不行,1个结点的树插入节点后,也只有2个结点(可能在左,也可能在右),根节点左右子树的差为1,还是棵平衡树。
如果这棵树有2个结点,那么树的形态必然是:根节点+左子树或右子树有1个结点。假设这个结点是根节点的左结点,如果插入1个结点,就会出现2种情况:
- 插入在左子树下,左子树是平衡树,但是根节点不平衡了(左子树高度为2,右子树高度为0,
D = 2) - 插入在根节点的右节点处,整棵树依然是平衡的;
2个结点的插入前和插入后的情况如图:
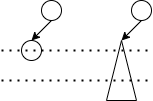
如果这棵树有3个结点,如果除了根节点外另外两个结点都在左子树,那么左子树会不平衡。我们要求插入节点前该树是平衡的,因此该情况不成立。如果必须根节点左右各1个结点,那么插入1个结点后,整棵树依然是平衡树。因此3个结点的情况不成立。
如果这棵树有4个结点。那么根节点占1个,其他两棵子树占3个。如果说3个结点都在根节点的左子树,那么左子树的高度至少为2,右子树的高度为0。那么该树不平衡,不符合我们插入前树必须是平衡的要求。因此只能是一边2个结点,另一边1个结点。假设左子树2个结点,右子树1个结点。插入新节点的时候,必须是在下一层,否则插入结点后的树依然平衡。
4个结点的插入前和插入后的情况如图:
.png)
综上,要满足插入前树平衡,插入后不平衡的要求,该树要么有2个结点,插在有结点的那棵子树上。要么有4个结点,插入的结点必须使得树新加一层。
等等!上面这个图好像有一些奇怪的地方!我们可以发现,对于4个结点的情况,在进行了如上插入以后,新形成的树的根结点,已经不再是出现刚出现不平衡点的结点了。不平衡树出现的结点,是根结点的孩子!而我们把根节点的孩子提出来,是这样的结构:
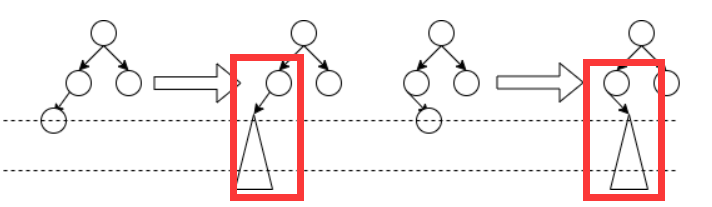
这不正是我们前文提到过的2个结点的树插入后的结构吗?
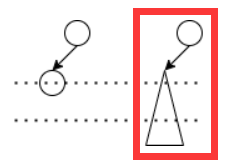
因此,插入的不平衡情况可以被分为4种(最右侧的为左边2图的简化图):
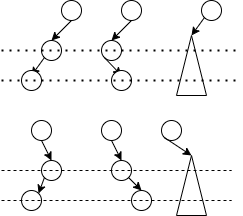
但是现在新的问题出现了,所有的情况都能被归类为这4种吗?会不会出现一种情况,平衡树的结点大于4个,在插入节点前,该树为平衡树。在插入节点后,该树为非平衡树。而且该树的根就是出现非平衡处的地方。我们发现对于5个结点插入的情况,仍然存在这样的树。即左子树有3个结点,分布在2层,右子树有1个结点。插入后排列如下(右图为左图简化版,囊括了插入在左右孩子的两种情况):
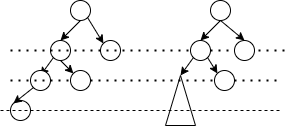
综上,我们可以进行如下总结,不平衡处出现在:
- 左孩子
- 右孩子
- 左孩子的左子树
- 左孩子的右子树
- 右孩子的左子树
- 右孩子的右子树
4.2 删除情况分析
结点的删除遵循搜索二叉树的结点删除过程。复习一下:
- 如果删除的是叶子节点,直接删除即可;
- 如果删除的不是叶子节点,分情况讨论
- 左子树不为空,就用左子树的最右结点替代它;
- 左子树为空,但是右子树不为空,就用右子树的最左节点替代它;
删除的结果和插入一样,可能出现不平衡树。此外,删除的情况和插入一样复杂,我们无法对每个具体的情形进行处理。此外,我们只知道删除后的树不是平衡树,而对删除前的树的长相无法预测。这里我们想要分析的是删除后不平衡树的处理,而其实在分析插入的时候,我们就已经归纳过几种不平衡树的形态。因为因此对于插入和删除,我们可以进行统一的处理,而无需考虑删除前的树的形态。
4.3 统一处理:4种情况
5 AVL树的旋转原理
要达成AVL树的效果,我们需要在对二叉树的结点进行插入和删除时增加一个操作,即"旋转"。
在旋转之前,我们需要找到不平衡树出现的那个根节点。其以上的树的不平衡都是由那个根节点下的左右子树导致的。下面的旋转操作均是围绕着这个出现不平衡情况的根节点实现,而不是围绕着整棵树的根节点。
如果一棵树插入节点后,成为了不平衡树,只可能是以下四种情况:
- 插入在左子树的左孩子;
- 插入在左子树的右孩子;
- 插入在右子树的左孩子;
- 插入在右子树的右孩子;
其中,情况1和4处理相似,2和3处理相似。对于情况1和4,只需要一次旋转。而对于情况2和3,需要2次旋转。
6 单旋转原理
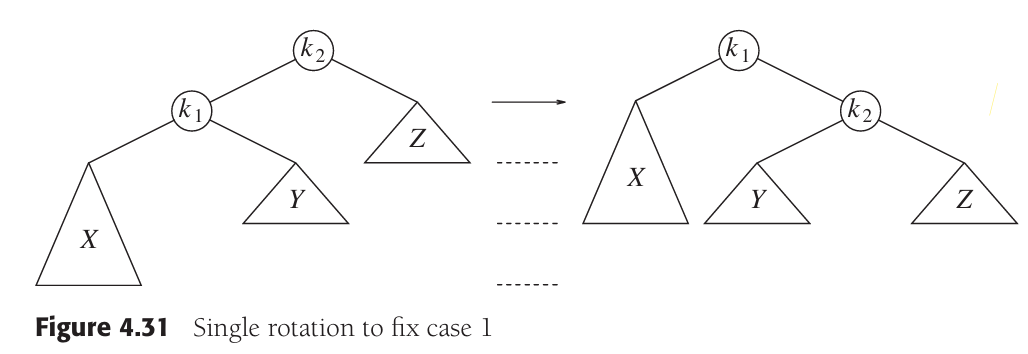
根据前文,单旋转有2种情况:
- 新结点插入在左子树的左孩子;
- 新节点插入在右子树的右孩子;
这两种情况实际上是相同的,我们以第一种为例来进行分析。我们通过旋转,将左图的情况转变为右图。因为k1为不平衡树的根节点,因此我们抓住k1,摇一摇,那么k2就落了下来,Z依然是k2的右节点,X依然是k1的左节点。那么Y怎么办呢?Y的值大于k1而小于k2,因此它转变为k2的左节点。
7 双旋转
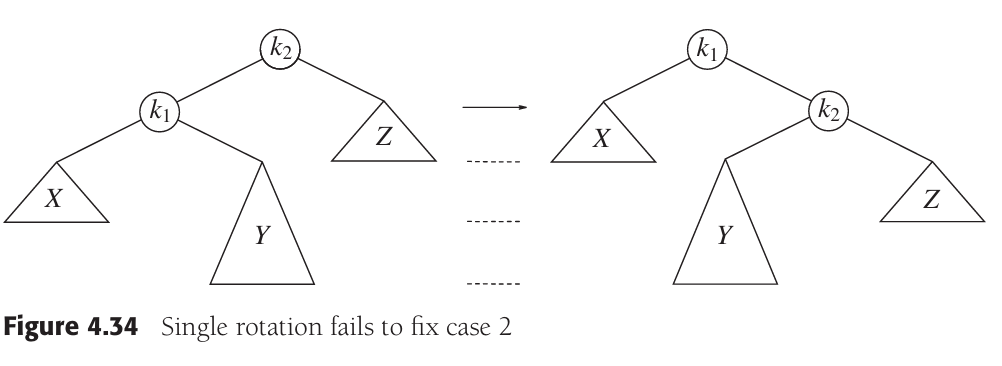
根据前文,双旋转有2种情况:
- 新节点插入在左孩子的右子树;
- 新节点插入在右孩子的左子树;
我们首先分析第一种方式。如果只是单旋转,旋转后如右图。我们可以看到,该树依然是不平衡的。k1是不平衡树的根。这样的单旋转只是把左图的样子做了个镜面效果罢了,归根结底是因为Y太深了。
对于Y,我们可以推测,其有一个根节点,和1-2个子节点。经过分析我们可以知道,Y的根节点的值是大于k1,小于k2的。那么我们可以把Y的根节点作为树的根节点,让k1和k2分别作为它的左右子树。又因为Y的左节点大于k1且小于Y的根节点,因此将其作为k1的右结点。同理,Y的右结点小于k2且大于Y的根节点,因此将其作为k2的左结点。
综合以上分析,我们对第一种情况进行如图的双旋转,成功解决问题(这里图中的根节点由k2替换成了k3,而k2表示Y的根节点,和上图的表示有一些区别,需要注意一下):
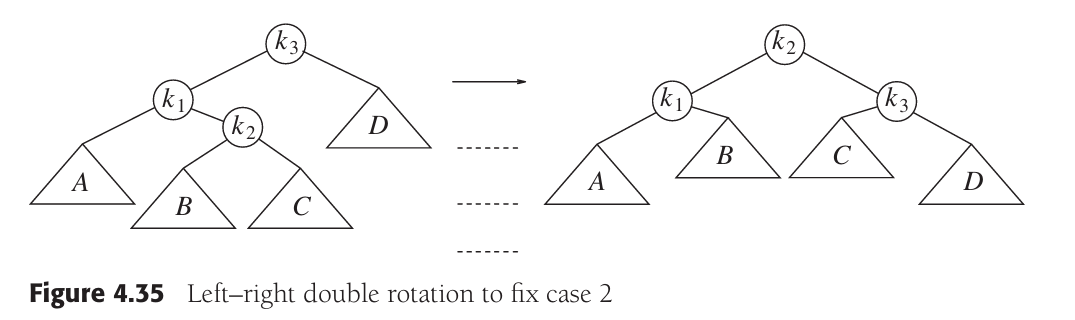
下面我们分析第二种形式,也就是新节点插入在右孩子的左子树。其总体思路和第一种形式相同。如图,我们将Y抽象为一个由根节点k2和两个子节点B和C构成的二叉树(实际C不一定存在,可能为空)。那么k2大于k1且小于k3,因此让k2作为新的平衡二叉树的根节点。而B大于k1且小于k2,因此B为k1的右节点。C大于k2且小于k3,因此C为k3的左节点。旋转效果如右图所示。