<Digital Design and Computer Architecture> MIPS 版本 阅读笔记
以下是 《Digital Design and Computer Architecture》 第 1-8 章的阅读笔记,目录采用原书结构,笔记内容为自己整理(3.5节 时序逻辑电路的时序特性分析跳过)。数字电路部分还可以参考这本教材:Fundamentals of Digital Logic with Verilog Design, THIRD EDITION (auhd.edu.ye)
1 Chapter 1:从 0 到 1
1.1 1.1 大纲
这一章主要为导引内容,比较简单,因此阅读笔记中仅介绍大纲和课后作业。
- Abstraction
- Dicipline
- 3Y’s Deisng Dicipline
- Hierarchy
- Modularity
- Regularity
- Digital Abstraction:From Analog to Digital System
- Number System
- Decimal Numbers
- Binary Numbers
- Hexdecimal Numbers
- Bytes, Nibbles and All that Jazz
- 8 bits -> bytes
- 4 bits -> nibble
- Data in chunks -> words -> depend on the architecture of the microprocessor
- Memory size -> bytes
- Communication speed -> bits/sec
- Arithmetic
- Unsigned numbers
- Binary Addition
- 溢出判断:使用全加器时,最高位是否为 1
- Binary Addition
- Signed Numbers
- Sign-magnitude representation
- 2’s complement representation
- 溢出判断:如果两数的符号位相同,最高位是否和他们不同
- Comparison of Number System
- Unsigned
- Sign-Magnitude
- 2’s Complement
- Logic Gates
- Or
- And
- Not
- Buffer
- Nand
- Xor
- Beneath the Digital Abstraction
- CMOS Transistors*
- Power Consumption*
2 Chapter 2:组合逻辑设计
这一章前面的布尔运算、公理和对偶式、卡诺图的使用、以及布尔代数到电路图的转换较为简单,因此不作详细说明,摆出重点公式和算法。
2.1 2.1 Introduction
组合逻辑电路主要有 4 个组成部分:
- 一个或多个输入
- 一个或多个输出
- 组合逻辑函数
- 表示组合逻辑延迟的时序
2.2 2.2 Boolean Equations
2.2.1 最小项
每个布尔变量,以原变量或者其反变量的形式,在各个&式中出现一次。真值表中输出为 1 的行,可以表示为所有这种&式的或。譬如有布尔变量A和B,其输出公式为$F(A,B)=\bar{A}B+AB$将每个&式表达为一个十进制的值(如 AB 对应0b11,其十进制的值为 3,该项就可以表示为m3),对他们进行|运算,这种表示就是最小项。其最小项公式可以表述为:
$F(A,B)=\Sigma(m1,m3)$
2.2.2 最大项
找到真值表中所有输出为 0 的行,将其中为 1 的布尔变量取反,和值为 0 的布尔变量相或。将每个这样的行的值相与,得到的就是最大项。
2.2.3 最大项和最小项的关系
- 最小项中的每一项结果都为 1,只要这些项有 1 个为 1,结果就为 1
- 最大项中每一项的结果都为 0,只要有一个项为 0,结果就为 0
- 最大项可以由最小项进行取反得到
2.3 2.3 Boolean Algebra
- 公理及其对偶式
- 单变量定理
- 多变量定理
- 真值表
- 简化真值表
2.4 2.4 From Logic to Gates
- 单输出的 Gates:单个逻辑表达式
- 多输出的 Gates:多个逻辑表达式
2.5 2.5 Multilevel Combinational Logic
- 硬件简化
- Bubble Pushing
2.6 2.6 X’s and Z’s, Oh My
X:
- 不合法的值,如输出同时出现 1 和 0,导致冲突
- 电路尚未初始化的值
- 卡诺图中的无关项(注意区分和电路中的区别) Z:
- 高阻态,非 0 也非 1
- 多见于三态门
2.7 2.7 Karnaugh Maps
- 一次在卡诺图中圈出一个大小为 1,2,4,8(或其他 2 的倍数)的块
- 每个圈都代表一个逻辑表达式
- 卡诺图的上下,左右的边缘相连
- 所有逻辑表达式的和就是,电路最后的简化逻辑表达式
2.8 2.8 Combinational Building Blocks
- 选择器
- 译码器
2.9 2.9 Timing
2.9.1 Propagation
- 传播延迟:从输入改变 -> 输出值完全稳定下来,中间所需要的时间,一个模块从输入到输出的传播延迟取决于最长的那条路径(关键路径)
- 最小延迟:从输入改变 -> 输出开始改变,中间所需要的时间
2.9.2 Glitches
- 竞争冒险:多见于关键路径和最短路径输出的值不一样,而其值到达输出的时刻不一样,导致输出电路的值出现波动。
- 竞争冒险的消除可以通过向电路中增加卡诺图中的冗余项实现。冗余项来源于卡诺图中两个圈相切的部分,将相切的部分的两个圈化为一个圈,将其添加到电路中,即可消除竞争冒险。
3 Chapter 3:时序逻辑设计
这一章的时序逻辑分析和设计较为重要,学习过程中可以参考这个油管系列视频: Sequential Circuits - YouTube
学习完成之后可以:
- 完成华科的数字逻辑设计头歌平台所有作业
- HDLBits Verilog语言学习
- Vivado/Quartus Verilog编程环境配置
- 其他学校的数字电路实验课完成
3.1 3.1 Introduction
- 组合逻辑电路的输出只和输入有关
- 时序逻辑电路的输出不只和输入有关,还和之前的状态相关
- 本章我们会
- 介绍时序逻辑电路的组成
- 状态变量的设计
- 介绍状态机
- 时序逻辑电路的效率
- 提高时序逻辑电路效率的方法:并行化
3.2 3.2 Latches and Flip-Flops
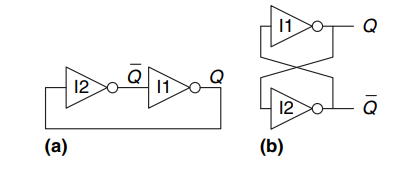
上图中表示的是一个维持稳定状态的电路,为什么说它们维持稳定状态呢?
- 对(a)中电路,如果 I2 的输入为 0,$\bar{Q}$为 1,I1 的输入为 0,又传回 I2,电路状态永远不变。当 I2 的输入为 1 时,同上。
- 对(b)中电路,如果 I2 的输入为 0,那么 I1 的输入为 1,Q 为 0,$\bar{Q}$为 1,电路状态保持不变;反之亦然。 在 Q 和$\bar{Q}$的值变化的过程中,可能存在其他的状态,这个情况我们在后面会进行讨论。
以上的电路有 2 个状态,可以承载 1 个 bit 的信息。那么 N 个状态的电路,就可以承载$\log_{2}N$个 bit 的信息。Q 是该电路的一个有效状态,$\bar{Q}$也可以说是一个有效状态,但是我们知道它是 Q 的取反,因此知道 Q 就够了。
但是这个电路的不足在于,我们不知道他是什么状态,我们无法输入,这个问题需要修复。
3.2.1 SR Latch

SR 锁存器特点:
- 2 个输入:S 和 R
- 2 个输出:Q 和$\bar{Q}$
SR 锁存器真值表:
- S=0,R=0
- N2 输出对 Q 取反,N1 输出对$\bar{Q}$取反。因为 N2 的输出原本就是$\bar{Q}$,N1 的输出原本就是 Q,因此状态不变
- S=0,R=1
- N1 输出 0(Q=0),N2 这里 Q 和 S 都是 0,因此输出 1($\bar{Q}$=1)
- S=1,R=0
- N2 输出 0($\bar{Q}$=0),N1 这里$\bar{Q}$和 R 都是 0,因此输出 1($Q$=1)
- S=1,R=1
- Q 和$\bar{Q}$都输出 0,冲突,这种情况不应当存在
因为 R=1 时 Q=0,S=1 时 Q=1,因此 S 和 R 称为 Set 和 Reset。
SR 锁存器有一些问题:
- S 和 R 都为 1 时发生冲突,因此不应该让 SR 同时为 1
- 当某个输入被设置为 1 时,状态立刻改变,我们应当对这个改变的时刻加以控制。输入的改变和状态的改变,应当分开进行控制。
3.2.2 D Latch

D 锁存器的出现是为了解决 SR 锁存器的上述两个问题,我们进行了两方面的调整:
- 引入输入 D
- 引入时钟信号 CLK,用 CLK 的高低控制锁存器的开闭
D 锁存器的工作机制和 SR 锁存器类似,当 CLK=1 时,S=$\bar{D}$,否则 SR 寄存器保持原有状态,这种机制称为level-sensitive latch,也就是锁存器状态取决于 CLK 为 1 时电平信号的高低。
D 锁存器也有一点小小的缺陷,也就是 CLK 为 1 时,锁存器的状态完全取决于 D 电平信号的高低。如果 D 的电平信号震荡,锁存器的状态也会随之上下改变。我们希望能够实现锁存器状态的稳定,让状态更新在一个时刻完成,而不是一段时间,要解决这个问题,下面我们引入 D 触发器。
3.2.3 D flip-flop

D 触发器由两个接入相反时钟状态的 D 锁存器构成,前一个称为master,后一个称为slave。其特性在于:
- 当 CLK=0 时,
master打入值,slave的值不随master改变 - 当 CLK=1 时,
slave打入值,master的值不随输入改变
因此,触发器的状态主要取决于 CLK 从 0 到 1 时,实现锁存器的状态转换,而其他时刻状态不变。这样就解决了 D 锁存器状态因转换的时间过长而带来的可能的状态震荡。该触发方式也叫边沿触发。
3.2.4 Register
寄存器由多个触发器组成,可以存储多位的值,每个触发器存储 1 位的值,通过给他们连接同步的时实现。
3.2.5 Enabled Flip-Flop

使能触发器在普通的 D 触发器的基础上,增加了一个 2 选 1 数据选择器。数据选择器的选择端是使能信号,两个数据信号分别是输入 D 和触发器的之前状态。
其状态如下:
- Enable = 1 时,使能触发器输入为 D
- Enable = 0 时,使能触发器保持之前状态
使能触发器相对于 D 触发器做出的改进在于:我们只有在希望的时候才打入输入,而不是在每次时钟上升沿都打入。其控制能力相比 D 触发器更上一层。
3.2.6 Resettable Flip-Flop

可复位触发器相比使能触发器的区别在于,当 reset 信号为 1 时,与门输出为 0,打入的信号为 0,状态更新为 0,实现状态复位。该设置常用于对触发器进行同步/异步复位。
3.2.7 Transistor-Level Latch and Flip-Flop Designs*
此段省略。
3.2.8 Putting It All Together
- D 锁存器:高电平触发
- D 触发器:时钟上升沿触发
3.2.9 Summary
下面我们对本章介绍的多个锁存器和触发器、以及寄存器进行介绍,最重要的是D 触发器。
- SR 锁存器:实现了过去状态的存储,但是 SR 均为 1 时电路无效,并且无法控制状态转换的时刻
- D 锁存器:解决了 SR=1 时的无效状态,引入 CLK 时钟对电路进行控制,但是状态变化的间隔过长,容易导致在高电平期间,电路状态随着输入变化而持续变化,我们希望在某个时刻完成状态转换,然后保持其不变
- D 触发器:采用
master-slave结构,master接$\bar{CLK}$,而slave接 CLK。master在低电平期间状态改变,其他时候不变。slave在高电平期间状态改变,其他时候不变。因此最终的结果是触发器的状态取决于时钟上升沿。但是在每次时钟上升沿,电路的状态都会随着输入的状态改变。因此我们希望设置一下电路是接受输入,还是保持状态不变 - D 使能触发器:在 D 触发器的基础上增加一个数据选择器,利用使能信号来选择下一个时钟上升沿,打入
slave的值是新的输入,还是电路之前的状态 - D 复位触发器:将 D 触发器的输入和$\bar{RESET}$进行与操作,如果
RESET = 1,那么$\bar{RESET} = 0$,输入为 0,实现了触发器的复位 - 寄存器:由多个触发器构成,每个触发器接的是相同的时钟
3.3 3.3 Synchronous Logic Design
3.3.1 3.3.1 Some Problematic Circuits
- 以一段时间为周期的周期性震荡的电路

- 存在因电路延迟带来的竞争冒险的电路

3.3.2 3.3.2 Synchronous Sequential Circuits
上述电路出现问题的原因:电路中出现了环路
如何消除环路?通过向环路中间加入寄存器,将环路转化成多个段,每个寄存器都由触发器组成,在时钟上升沿触发,因此我们说该电路是时钟同步电路,以此为基础,我们设计了时序逻辑电路。
时序逻辑电路有 5 个组成要素:
- 多个中间状态
- 输入
- 输出
- 组合逻辑函数
- 时序,即一个同步的 CLK
- 时钟上升沿 -> 输出开始变化:$T_{setup}$
- 时钟上升沿 -> 输出值稳定:$T_{hold}$
时序逻辑电路的特点在于:
- 由寄存器(触发器,不是锁存器)和组合逻辑电路组成
- 至少有一个寄存器(触发器,不是锁存器)
- 所有寄存器接受相同的时钟信号(不可以有延迟)
- 每个环路至少有一个寄存器
3.3.3 3.3.3 Synchronous and Asynchronous Circuits
异步时序逻辑电路比同步时序逻辑电路更常见,但是更复杂。这里不详述。
3.4 3.4 Finite State Machines
时序逻辑电路可以被表示成有限状态机的形式,它通常有如下几个组成部分:
- M 个输入
- N 个输出
- k 位的状态(因此电路一共可以有$2^{k}$个状态)
- 一个时钟
时序逻辑电路又分两种:
- Moore 型电路:电路的状态由电路之前的状态和组合逻辑函数决定
- Mealy 型电路:电路的状态由之前的状态,电路的输入,和组合逻辑函数决定

3.4.1 3.4.1 FSM Design Example
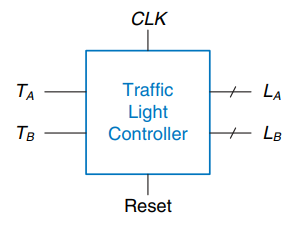
下面通过一个设计十字路口交通灯的案例,来演示时序逻辑电路的设计。
3.4.1.1 步骤一:明确问题背景
- 十字路口有两个传感器:$T_{A}$和$T_{B}$,当传感器输出为
True代表有学生,输出为False代表道路空 - 两个交通灯:$L_{A}$和$L_{B}$,每个交通灯都要接受传感器的数据,然后决定是输出
红,绿,还是黄 - 每个交通灯有 5 秒的间隔,交通灯在时钟上升沿通过传感器的输入,更新自己的状态
- 控制器还有一个 reset 按钮来实现复位
交通灯概念图设计如下:

交通灯接口设计如下:
3.4.1.2 步骤二:绘制状态转换图
电路状态转换过程分析如下:
- 状态的初始值(复位状态)如下:A 路绿,B 路红
- 如果$T_{A}$为
True,那么 A 路持续绿,B 路持续红;否则,A 路进入黄色,B 路红 - A 路黄,B 路红时,我们无需管$T_{A}$的状态。过 5 秒自动切入下一个状态:A 路红,B 路绿
- A 路红,B 路绿时,如果$T_{B}$为
True,那么 A 路持续红,B 路持续绿;否则,A 路红,B 路进入黄色 - A 路红,B 路进入黄色时,我们无需管$T_{B}$的状态,过 5 秒后回到初始状态,A 路绿,B 路红
根据以上分析,电路可以划分为以下几个状态:
- A 路绿,B 路红:$T_{A}$为
True时保持,否则进入状态 2 - A 路黄,B 路红:5 秒后进入状态 3
- A 路红,B 路绿:$T_{B}$为
True时保持,否则进入状态 4 - A 路红,B 路黄:5 秒后进入状态 1
 电路转换的时机是时钟上升沿
电路转换的时机是时钟上升沿
3.4.1.3 步骤三:绘制状态转换表
我们将状态转换图,转化为状态转换表。在绘制过程中,我们需要明确如下几样:
- 状态表示:这里我们用 S0,S1,S2,S3 来表示
- 状态转换输入:用$T_{A}$,$T_{B}$来表示,使用 X 来表示无关项(类似卡诺图)
状态转换表的每行有 3 项:
- 该状态
- 输入
- 下一状态
绘制状态转换表如下:
| 当前状态 | 输入$T_{A}$ | 输入$T_{B}$ | 下一状态 |
|---|---|---|---|
| S0 | 0 | X | S1 |
| S0 | 1 | X | S0 |
| S1 | X | X | S2 |
| S2 | X | 0 | S3 |
| S2 | X | 1 | S2 |
| S3 | X | X | S0 |
3.4.1.4 步骤四:对状态进行二进制编码
状态分为:S0,S1,S2,S3
| 状态 | $S_{1}$ | $S_{0}$ |
|---|---|---|
| S0 | 0 | 0 |
| S1 | 0 | 1 |
| S2 | 1 | 0 |
| S3 | 1 | 1 |
3.4.1.5 步骤五:对输出进行二进制编码
输出分为:红、黄、绿
| 输出 | $L_{1}$ | $L_{0}$ |
|---|---|---|
| 绿 | 0 | 0 |
| 黄 | 0 | 1 |
| 红 | 1 | 0 |
3.4.1.6 步骤六:确定状态与输入关系表(将状态编码嵌入到状态转换表)
| 当前状态 | $S_{1}$ | $S_{0}$ | 输入$T_{A}$ | 输入$T_{B}$ | 下一状态 | $S_{1}$ | $S_{0}$ |
|---|---|---|---|---|---|---|---|
| S0 | 0 | 0 | 0 | X | S1 | 0 | 1 |
| S0 | 0 | 0 | 1 | X | S0 | 0 | 0 |
| S1 | 0 | 1 | X | X | S2 | 1 | 0 |
| S2 | 1 | 0 | X | 0 | S3 | 1 | 1 |
| S2 | 1 | 0 | X | 1 | S2 | 1 | 0 |
| S3 | 1 | 1 | X | X | S0 | 0 | 0 |
3.4.1.7 步骤七:确定状态与输出的关系表(根据电路分析、状态编码和输出编码)
| 状态 | $S_{1}$ | $S_{0}$ | $L_{A1}$ | $L_{A0}$ | $L_{B1}$ | $L_{B0}$ |
|---|---|---|---|---|---|---|
| S0 | 0 | 0 | 0 | 0 | 1 | 0 |
| S1 | 0 | 1 | 0 | 1 | 1 | 0 |
| S2 | 1 | 0 | 1 | 0 | 0 | 0 |
| S3 | 1 | 1 | 1 | 0 | 0 | 1 |
3.4.1.8 步骤八:写出状态表达式
我们使用$S’$来表示下一时刻的状态,可以如下表示:
$$ S_{1}’ = S_{1}S_{0} +S_{1}S_{0}T_{B} +S_{1}S_{0}T_{B} $$
$$ S_{0}’ = S_{1}S_{0}T_{A}+S_{1}S_{0}T_{B} $$
3.4.1.9 步骤九:写出输出表达式
$$ L_{A1} = S_{1}L_{A0} = S_{1}S_{0} $$
$$ L_{B1} = S_{1}L_{B0} = S_{1}S_{0} $$
3.4.1.10 步骤十:画出电路图
设计寄存器
 状态寄存器设计如图,左边是下一时刻状态,右边是之前的状态。在时钟上升沿,下一时刻状态打入寄存器,因此将其花在左边,而不是右边。
状态寄存器设计如图,左边是下一时刻状态,右边是之前的状态。在时钟上升沿,下一时刻状态打入寄存器,因此将其花在左边,而不是右边。添加状态与输入关系电路

添加状态与输出关系电路

3.4.2 3.4.2 State Encodings
状态编码有分为二进制编码(binary encoding)和独热编码(One-hot encoding)
3.4.2.1 Binary Encoding
N 个编码只需要$log_{2}N$位就可以表示。
3.4.2.2 One-hot Encoding
N 个编码需要 N 位二进制表示,该二进制数中,对于一个状态有且仅有 1 位的值为 1。选择这种编码需要更多的触发器,但是对应的输出电路和状态转换电路会更简单。
3.4.2.3 设计示例1:3进制计数器
设计一个 divide by 3 counter,当状态转换的次数为3的倍数时(对3求模 = 0),输出为1,否则输出为0
3.4.2.3.1 背景分析
根据分析,电路存在3个状态:
- S0:初始状态,也是最终状态,输出为1。下一时刻跳转到S1
- S1:输出为0,下一时刻跳转到S2
- S2:输出为0,下一时刻跳转到S0
电路状态转换图如下:

3.4.2.3.2 状态转换图绘制

状态有3个,S0、S1和S2,我们分别采用二进制编码和独热编码对其进行编码。
3.4.2.3.3 采用二进制编码设计
- 状态编码:电路有3个状态,我们采用2位二进制进行编码,分别用$S_{1}$和$S_{0}$表示。
| 状态 | $S_{1}$ | $S_{0}$ |
|---|---|---|
| S0 | 0 | 0 |
| S1 | 0 | 1 |
| S2 | 1 | 0 |
- 输出编码:电路只有1个输出,也就是Y,那么我们只需要1位二进制数表示
- 状态转换表
| 状态 | $S_{1}$ | $S_{0}$ | 下一状态 | $S_{1}'$ | $S_{0}'$ |
|---|---|---|---|---|---|
| S0 | 0 | 0 | S1 | 0 | 1 |
| S1 | 0 | 1 | S2 | 1 | 0 |
| S2 | 1 | 0 | S0 | 0 | 0 |
由图我们可以得到状态表达式,下一时刻的状态用$S’$表示。
$$ S_{1}’ = \bar{S_{1}}S_{0} $$
$$ S_{0}’ = \bar{S_{1}}\bar{S_{0}} $$
- 状态与输出关系表
| 状态 | $S_{1}$ | $S_{0}$ | 输出Y |
|---|---|---|---|
| S0 | 0 | 0 | 1 |
| S1 | 0 | 1 | 0 |
| S2 | 1 | 0 | 0 |
由图我们可以得到输出与状态的关系式:
$$ Y=\bar{S_{1}}\bar{S_{0}} $$
- 电路图设计

3.4.2.3.4 采用独热编码设计
- 状态编码:独热编码对每个状态使用1位单独的二进制1,因此3个状态需要3位二进制数。
| 状态 | $S_{2}$ | $S_{1}$ | $S_{0}$ |
|---|---|---|---|
| S0 | 0 | 0 | 1 |
| S1 | 0 | 1 | 0 |
| S2 | 1 | 0 | 0 |
- 输出编码:电路只有1个输出,也就是Y,使用1位二进制数表示
- 状态转换表
| 状态 | $S_{2}$ | $S_{1}$ | $S_{0}$ | 下一时刻状态 | $S_{2}'$ | $S_{1}'$ | $S_{0}'$ |
|---|---|---|---|---|---|---|---|
| S0 | 0 | 0 | 1 | S1 | 0 | 1 | 0 |
| S1 | 0 | 1 | 0 | S2 | 1 | 0 | 0 |
| S2 | 1 | 0 | 0 | S0 | 0 | 0 | 1 |
由图我们可以得到状态表达式:
$$ S_{1}’ = S{0} $$
$$ S_{2}’ = S{1} $$
$$ S_{0}’ = S{2} $$
- 状态与输出关系表
| 状态 | $S_{2}$ | $S_{1}$ | $S_{0}$ | 输出Y |
|---|---|---|---|---|
| S0 | 0 | 0 | 1 | 1 |
| S1 | 0 | 1 | 0 | 0 |
| S2 | 1 | 0 | 0 | 0 |
由此我们可以得到状态与输出表达式:$Y=S_{0}$
- 电路设计
通过上面的分析,我们可以看到,独热编码的逻辑表达式比二进制编码要简单很多,但是会更加消耗二进制位数。电路设计如下:

3.4.2.4 设计示例2:3进制累加器
设计一个累加器,当连续输入3个1时,输出为1,其他时候输出为0。
3.4.2.4.1 背景分析
根据分析,电路存在3个状态:
- S0:起始(复位)状态,输入0个3时,输出为0。若此时输入1,进入S1;否则继续S0
- S1:输入1个3时,输出为0。若此时输入1,进入S2;否则进入S0
- S2:输入2个3时,输出为0。若此时输入1,进入S3;否则进入S0
- S3:输入3个3时,输出为1。下一状态为S0
3.4.2.4.2 状态转换图绘制
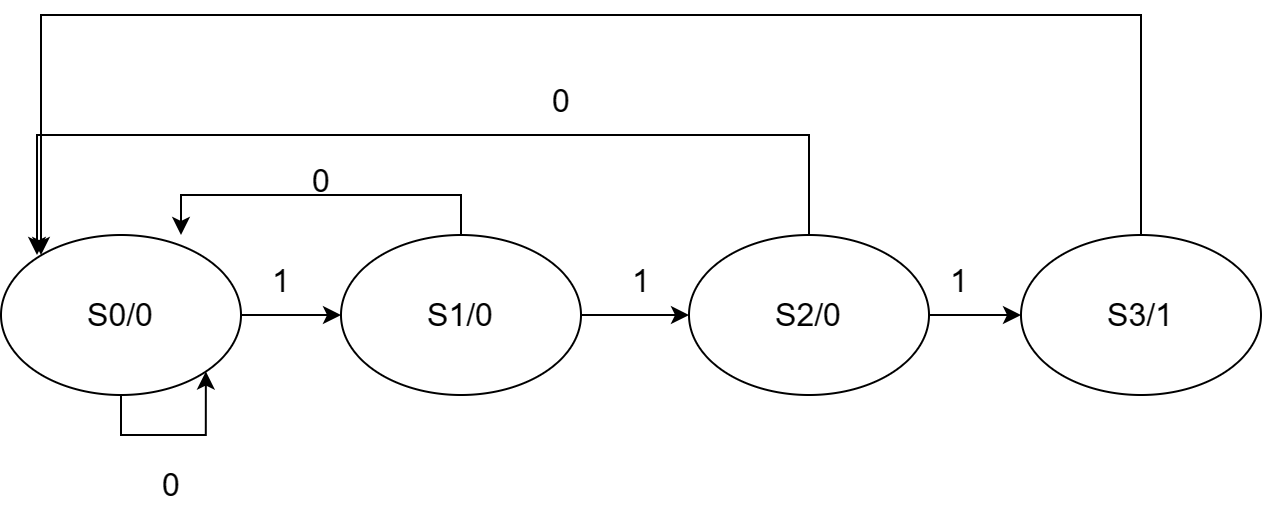
3.4.2.4.3 状态转换表绘制
| 状态 | $S_{1}$ | $S_{0}$ | 输入T | 下一时刻状态 | $S_{1}'$ | $S_{0}'$ | 输出 |
|---|---|---|---|---|---|---|---|
| S0 | 0 | 0 | 0 | S0 | 0 | 0 | 0 |
| S0 | 0 | 0 | 1 | S1 | 0 | 1 | 0 |
| S1 | 0 | 1 | 0 | S0 | 0 | 0 | 0 |
| S1 | 0 | 1 | 1 | S2 | 1 | 0 | 0 |
| S2 | 1 | 0 | 0 | S0 | 0 | 0 | 0 |
| S2 | 1 | 0 | 1 | S3 | 1 | 1 | 0 |
| S3 | 1 | 1 | X | S0 | 0 | 0 | 1 |
3.4.2.4.4 二进制编码实现
- 状态编码:状态有4个,因此使用2位二进制数进行编码
| 状态 | $S_{1}$ | $S_{0}$ |
|---|---|---|
| S0 | 0 | 0 |
| S1 | 0 | 1 |
| S2 | 1 | 0 |
| S3 | 1 | 1 |
输入编码:输入只有1个,因此使用1位二进制数表示
输出编码:输出只有1个,因此使用1位二进制数表示
状态转换表达式 $S_{1}’=\bar{S_{1}}S_{0}T + S_{1}\bar{S_{0}}T$ $S_{0}’=\bar{S_{0}}$
输出表达式:$Y=S_{1}S_{0}$
此处不画电路图。
3.4.3 3.4.3 Moore and Mealy Machines
详细的案例可见教材P132面蜗牛爬行问题。
Mealy型电路相比Moore型电路的主要区别在于,它的输出不仅取决于之前的状态,还取决于输入。通常在设计Mealy型电路的状态转换图时,我们会使用较少的状态,将状态之间的输入和输出用输入/输出的方式写在状态转换弧线上。此外,因为输出跟输入有关,因此有时我们会直接用与门来确定输出。这样做带来的好处是,相比Moore型电路中,一定要等到状态确定才能确定输出,Mealy型电路的输出少了一个触发器(寄存器)的延迟。

3.4.4 3.4.4 Factoring State Machines
当遇到比较复杂的问题时,我们需要将问题分解为多个状态机,将一个状态机的输出作为另一个状态机的输入,而不是使用一个状态机解决。这种做法会带来相当程度的简化。


3.4.5 3.4.5 Deriving an FSM from a Schematic
本节介绍如何由时序逻辑电路电路还原状态机,并且分析电路功能,这节的内容主要在于对电路的逆向工程。详细的案例可参考课本P137
- 分析电路的输入、输出、状态位
- 写出状态转换逻辑表达式,和输出逻辑表达式
- 根据表达式构建状态转换真值表,输出逻辑真值表
- 消除真值表中不存在的状态项(因为如果使用二进制表示法编码的话,二进制位可以产生的状态个数可能会大于实际需要的状态个数)
- 给每个有效状态分配一个状态名
- 将原来的状态转换表和输出表中的二进制编码替换为状态名
- 画出状态转换图
- 语言描述状态机的用途
3.4.6 3.4.6 FSM Review
本节介绍如何实现一个时序逻辑电路。
- 确定输入和输出
- 画出状态转换图
- 对于Moore型电路
- 写出状态转换表
- 写出输出逻辑表
- 对于Mealy型电路
- 写出一个状态转换表,其中合并了状态转换和输出
- 选择状态编码
- 写出状态转换逻辑函数和输出逻辑函数
- 画出电路图
3.5 3.5 Timing of Sequential Logic
这一段写得非常绕,但是我在找了几个油管的视频之后理解了,视频链接如下:

首先,我们需要了解一个原则,就是CLK时钟从0到1的变化,并不是突然之间产生的,而是经过一个短暂的阶梯型变化过程。从第一章的内容我们可以知道,模拟电路到数字电路的转换之前,需要对高电平和低电平进行定义。在某个电压之上,我们将其状态定义为高电平;在某个电压之下,我们将其定义为低电平;而在这之间,电平处于无效状态。
触发器的状态更新,就是发生在时钟上升沿。但是触发器并不是一个单一的部件,其由内部多个逻辑门所构成。如D触发器的结构如下:

在CLK位于低电平时,输入从D到N1,需要经过一个D锁存器。从N1到Q,需要经过一个D锁存器。我们需要保证触发器中的值(也就是slave锁存器中的值)是稳定的,那么就要求从D输入到N1,以及N1输入到Q的过程中,这个值保持稳定。从D输入到N1的时间,我们称为setup time;从N1到Q的时间,我们称为hold time。也就是说,输入必须在setup time + hold time期间内,保持稳定。不稳定所带来的情况,我们将在3.5.4 Metastability一节中讨论。
setup time和hold time之和也叫aperture time
3.5.1 3.5.1 The Dynamic Discipline

结合上述电路图,我们阐述几个重要的时间:
- contamination delay($t_{ccq}$):从上升沿获取输入,到得到Q1输出的最短时间
- propagation delay($t_{pcq}$):从上升沿获取输入,到得到Q1输出的最长时间
- setup time:在CLK上升沿之前,输入至少保持
setup time - hold time:在CLK上升沿之后,输入至少保持
hold time - 组合逻辑电路的延迟($t_{pd}$):值从Q1到Q2的最大时间
3.5.2 3.5.2 System Timing
在对电路的时序进行分析之前,我们需要明确两个值:$T_{c}$和$f_{c}$。前者是指两个时钟上升沿之间的时间间隔,也叫时钟周期。后者是前者的倒数,是时钟频率。时钟频率的增加,可以带来吞吐量的增加。时钟频率的单位包括:Hz,MHz和GHz。其单位换算如下:
- 1 megahertz (MHz) = 106 Hz
- 1 gigahertz (GHz) = 109 Hz.
结合上述电路块的结构分析,一个电路的值传递有如下几个阶段:
- 从输入,经过触发器R1,到Q1
- 从Q1,经过组合逻辑电路,到D2
- 从D2输入到触发器R2
3.5.2.1 Setup Time Constraint
在对约束条件进行分析时,我们采用
worst case analysis,也就是分析极限情况下的边界条件。需要注意的是setup time constraint指的不是setup time,而是对组合逻辑电路最大值的限制,因为组合逻辑部分是这个电路唯一可以优化的部分。
对电路setup time的约束主要在于触发器R2。分析如下:
- 在时钟上升沿后,触发器R1的值最多需要经过$t_{pcq}$才能到达Q1
- Q1的值最多需要经过$t_{pd}$才能到达D2
- 总的时钟周期为$T_{c}$
而D2输入必须满足setup time的要求,也就是说:
- D2的输入必须至少在时钟上升沿前$t_{setup}$刻开始保持稳定,即组合逻辑电路的值必须在$T_{c} - t_{setup}$时刻或之前抵达D2
综上分析,我们可以得出以下公式:
$t_{pcq}+t_{pd}<=T_{c}-t_{setup}$
通过移项运算,我们可以得到如下公式:
$$ T_{c} >= t_{pcq}+t_{pd}+t_{setup} $$
那么,$T_{c}$的值至少为$t_{pcq}+t_{pd}+t_{setup}$,那么$f_{c}$的值最大为
$$ f_{c} = \frac{1}{t_{pcq}+t_{pd}+t_{setup}} $$
通过这个公式,我们可以了解到,该电路的主要可优化部分为组合逻辑部分,$t_{pd} ≤T_{c}−t_{pcq} +t_{setup}$ 称为setup time constraint。
3.5.2.2 Hold Time Constraint
对于hold time的约束条件探索,我们同样采用取极端情况的情况,就是不考虑组合逻辑(其延迟为0)。
对于R2的输入D2,其之前的值需要保存$t_{hold}$个单位的时间。但是从R1过来的值,最短只需要$t_{ccq}+t_{cd}$个时刻就能到达,因此可以得出以下表达式:
$$ t_{ccq}+t_{cd}>=t_{hold} $$
因此,可以得出如下表达式:
$$ t_{cd} ≥ t_{hold}-t_{ccq} $$
组合逻辑电路延迟的最小值是 $t_{hold}-t{ccq}$。当两个触发器直接相接的时候,$t_{ccq}=0$,那么要求$t_{hold}<=t_{ccq}$。通常情况下我们默认$t_{hold}=0$,那么上述不等于恒成立。但是如果该条件不成立,我们就需要增加$t_{ccq}$,这需要对电路进行大量的修改,并且耗费巨大的资金,因此我们在设计电路时需要谨慎地考虑$t_{hold}$约束。
3.5.2.3 Putting It All Together
时序分析案例见课本P145面
两条约束原则:
- $t_{pd} ≤T_{c}−t_{pcq} +t_{setup}$
- $t_{cd} ≥ t_{hold}-t_{ccq}$
修复hold time violation,可以用加buffer的方式。但是要注意的是,有的时候加了Buffer后会改变关键路径,从而改变setup time的约束情况。
3.5.3 3.5.3 Clock Skew
这一段也不太好理解,尤其是hold time的部分,我参考了以下油管视频:

Clock skew的含义是:对各个触发器时钟上升沿到达的时间不一致。
产生clock skew的原因包括:
- 通往多个clock的线的长度不一致
- 噪声(
Noise) clock gating
在讲解Clock Skew之前,我们需要再看一下电路图:

对于一个触发器,master的CLK是通过slave的CLK取反得到的,因此这个非门可能会导致两个CLK的上升沿不一致,如图:

因CLK1比CLK2多经过1个非门,因此时钟到达CLK2的时间更早,CLK1更晚
3.5.3.1 setup time constraint分析
我们从worst case scenario分析(这里的worst case scenario指的是触发器输出和组合逻辑传递都取最长时间。因为我们要探索的是,在CLK1和CLK2的时钟上升沿间隔缩短,触发器输出和组合逻辑传输时间最长的情况下,依然保证留有$t_{setup}$个单位的时间,供R2维持输入的稳定):
- 从CLK1的上升沿开始,R1的值经过最多$t_{pcq}$进入到Q1;
- 经过组合逻辑的电路的延迟$t_{pd}$,Q1传输到D2,
- D2输入至少要在CLK2的上升沿前$t_{setup}$时刻达到,甚至更早
也就是说,从CLK1的上升沿,至少经过$t_{pcq}+t_{pd}+t_{setup}$抵达CLK2的上升沿。而从CLK1的上升沿到CLK2的上升沿,经过的时间是$T_{c}-t_{skew}$
经过如上分析,我们可以建立不等式:
$$ T_{c} - t_{skew} >= t_{pcq} + t_{pd} + t_{setup} $$
对其进行移位变换,我们可以得到:
$$ T_{c} >= t_{pcq} + t_{pd} + t_{setup} + t_{skew} $$
同上,setup time constraint指的是组合逻辑电路的延迟限制(因为组合逻辑电路是电路中唯一一个可以优化的部分,其他的时钟频率、触发器时延、时钟时延、setup time 都是不可改变的),我们可以得到如下不等式:
$$ t_{pd} <= T_{c} - (t_{pcq}+t_{setup}+t_{skew}) $$
3.5.3.2 hold time constraint分析
对于hold time constraint,我们同样分析的是R2,R2的值必须在CLK2时钟上升沿后,R1传过来的值到达前,保持至少hold time个时间单位。我们依然从worst case scenario分析(这里与setup time constraint的worst case不同,我们需要探测从R1传输过来的时间最短的情况,必须要让hold time比最短的传输时间还短,否则会导致hold time violation):
- R1的输出最少需要$t_{ccq}$个时间单位进入Q1
- Q1最少需要$t_{cd}$个时间单位进入D2
但是,因为有了clock skew。因此,哪怕信号已经到达了,而且CLK1已经经过了一个时钟周期,它也还需要再等待$t_{skew}$个单位的时间,才能进入R2。这为R2的$t_{hold}$争取到了一些额外的时间。
那么,我们就可以得到如下不等式:
$$ t_{hold} + t_{skew} <= t_{ccq} + t_{cd} $$
同上,组合逻辑电路是这个电路中唯一可以优化的部分,组合逻辑电路的时延要求如下:
$$ t_{cd} >= t_{hold} + t_{skew} - t_{ccq} $$
3.5.3.3 Put it all together
在存在clock skew的情况下,我们得到了两个不等式,描述了对于组合逻辑延迟的约束:
$$ t_{pd} <= T_{c} - (t_{pcq}+t_{setup}+t_{skew}) $$
$$ t_{cd} >= t_{hold} + t_{skew} - t_{ccq} $$
通过如上不等式,我们可以看到,clock skew使得组合逻辑电路的最大值减少、最小值增加。者带来的问题是,当两个触发器直接相接(无组合逻辑电路时),$t_{cd}=0$,$t_{skew}-t{ccq}$如果大于0,哪怕$t_{hold}$等于0,都会导致hold time violation。因此,很多厂家会把$t_{ccq}$设计的比较大,哪怕$t_{skew}$的值有时并不大,但是一旦导致hold time violation,修改电路导致的各方面的损失是巨大的。
带有
clock skew的时序电路分析案例见课本P150面。
对于存在hold time violation的电路,修复的方法包括:
- 加buffer(关键路径也要加)
- 改进触发器,将
hold time缩短 - 增加$t_{ccq}$
3.5.4 3.5.4 Metastability
这个油管视频讲的非常好:
3.5.4.1 Metastable State
Metastability指的是亚稳态,亚稳态指的是,输入在setup time和hold time内没有保持稳定,这导致输出不确定。输出可能会在0和$V_{DD}$之间(即forbidden zone),但是最终总会达到0或者1。
3.5.4.2 Resolution Time
我们把电路从亚稳态到稳态的时间记为$t_{res}$,有如下两种情况:
输入的变化是在
aperture time之外发生的,那么$t_{res} = t_{ccq}$否则,时间无法估计,只能用一个概率函数表示:
$$ P(t_{res}>t) = \frac{T_{0}}{T_{c}}e^{-\frac{t}{τ}}
$$ 这个概率函数的推导在这里意义不大,因此不与呈现。但是可以看到的是,这个概率是一个以$e$为底的指数函数,并且指数是负数,那么随着$t$增大,这个概率会以指数级别的速度减小,但是它不可能为0。
从第一章的介绍中我们可以知道,模拟电路到数字电路的映射方式是,将某个电压以上均视为高电平,某个电压以下均视为低电平,中间的称为forbidden zone。因此,电压无需完全的达到0,只需要最终下降到一个合理的区间内即可。随着时间的推移,电路极大可能处于稳态。
3.5.5 3.5.5 Synchronizers
在设计电路时,有时我们需要设计多个模块,这些个模块在时钟上可能不是完全同步的。或者,我们设计了一个同步电路,但是电路的输入是随机发生的,不一定会在aperture time内保持稳定,但是我们需要保证输出处于稳态,这时候就需要用到同步器。一个同步器有一个输入,一个CLK时钟,和一个输出,如图所示:
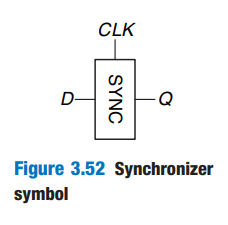
一个可能的同步器的实现就是将两个触发器直接相接,得到的电路如下:

在上述电路中,如果输入在aperture time中保持稳定,那么输出自然保持稳定。如果输入不稳定,如果给的时间够长,它极大概率会在$t_{res}$内转换到稳态。
对于无法转换到稳态的概率计算,详见课本P153面
3.5.6 3.5.6 Derivation of Resolution Time*
此节为前文$t_{res}$公式的推导,本节涉及到模拟电路的内容,此处略过。
3.6 3.6 Parallelism
参考了课程官方讲解视频:
此节有几个重要概念:
- 延迟(
latency):完成一项工作所花费的时间 - 吞吐量(
throughoutput):单位时间内完成工作的量
为了提高吞吐率,我们可以采用并行(parallelism)的方式,parallelism有两种:
spatial parallelism:复制硬件temporal parallelism:将工作拆分为多个阶段,不同的工作可能处于不同的阶段中,即流水线
量化分析,假设如下场景:
- 一个任务的延迟是L(完成一项任务所花费的时间是L)
- 它的吞吐量是1/L(在单位时间内完成的工作量是1/L)
对于spatial parallelism的系统,假设硬件复制了N份,那么:
- 任务的延迟依然是L
- 它的吞吐量是N/L(同一时刻有N份硬件完成该任务)
对于temporal parallelism的系统,假设把他划分为N个阶段,那么:
- 任务的延迟依然是L
- 对于流水线,第一个任务完成所需要的时间是L,自那以后每过L/N个单位的时间,就有一项任务完成。对于$n$个任务来说,完成所需要的总时间是$L+(N-1)\frac{L}{N}$,那么它的吞吐量就是$\frac{n}{L+(N-1)(\frac{L}{N})}$,对该式进行化简,过程如下: $$
\frac{n}{L+(N-1)*(\frac{L}{N})} = \frac{n}{2L-\frac{L}{N}}
$$
对于流水线来说,其一个阶段的时钟周期,取决于这个阶段中关键路径所花的时间(也就是从上个寄存器到下个寄存器,通过最长时间的路径);其延迟是指从流水线开头到流水线结尾所花费的时间;其吞吐量可以约等于$\frac{1}{时钟周期}$
temporal parallelism和spatial parallelism相比,其优势在于其可以通过不增加硬件达到加倍的吞吐量。
3.7 3.7 Summary
本章介绍了:
- 时序逻辑电路和组合逻辑电路的区别
- 多种锁存器 -> 多种触发器 -> 使能触发器和复位触发器
- 从状态转换图到时序逻辑电路的设计
- 时序逻辑电路的时序分析
- 多种
parallelism:spatial parallelism和temporal parallelism的延迟和吞吐量
3.8 Exercises
触发器的转换方法参考链接各类触发器的转换-数字电子技术-电子发烧友网站 (elecfans.com)
3.8.1 基础的锁存器 & 触发器特性
- SR锁存器
- S为set,S=1时,输出信号为1
- R为reset,R=1时,输出信号为0
- SR=1时,电路状态无效
- SR=0时,电路状态保持不变
- D锁存器
- CLK=1时,输出Q=D
- CLK=0时,输出保持不变
- D触发器
- CLK上升沿把D的值输入到Q
- 其他时候输出保持不变
3.8.2 各类触发器之间的互相转换
没有在课本中提到的是一些其他的触发器,以及触发器的特性方程,而触发器之间的互相转换需要利用到特性方程。特性方程指的是锁存器/触发器的下一时刻输出$Q*$与输入信号之间的关系。
- RS触发器:输入信号R和S,输出为Q*。特性方程为$Q^{*}=S+\bar{R}Q$
- D触发器:输入信号D和CLK,输出为Q*。特性方程为$Q^{*} = D$
- JK触发器:功能最强大
- JK都为0,保持输入
- J=1,输出为1
- K=1,输出为0
- JK都为1,输出取前一个时刻输出的取反
- 输入信号为J和K,输出为$Q^{}$,特性方程为$Q^{}=J\bar{Q}+\bar{K}Q$
- T触发器:
- 功能是每个时钟上升沿,输出为前一个时刻输出的取反。输入信号为T和CLK,输出为Q*;
- 特性方程为$Q^{*}=\bar{T}Q+T\bar{Q}$
各个触发器的状态转换的方法在于,用已知的触发器去表达未知的触发器,如下:
- D触发器 -> T触发器(用T表示D):$D=\bar{T}Q+T\bar{Q}$
- D触发器 -> JK触发器(用JK表示D):$D=J\bar{Q}+\bar{K}Q$
- JK触发器 -> D触发器(用D表示JK):
- 可以将D转化为$Q^{*}=D(Q+\bar{Q})=DQ+D\bar{Q}$
- 因为JK触发器特性方程为$Q^{*}=J\bar{Q}+\bar{K}Q$
- 那么$J=D,K=\bar{D}$
- JK触发器 -> T触发器(用T表示JK):
- JK触发器:$Q^{*}=J\bar{Q}+\bar{K}Q$
- T触发器:$D=\bar{T}Q+T\bar{Q}$
- 那么$J=T,K=T$
3.8.3 同步电路 vs 异步电路
异步
preset & clear电路的工作时序可以参考这个油管视频:
preset & clear latch/flip-flop的设计可以参考这个油管视频:以及这个油管视频:
查找异步视频资料的时候还费了点功夫,一开始搜索的是
asynchronous d latch/flip flop/sequential circuit design,结果搜到的资料非常有限,直到搜到一本sequential circuit design还是什么教材,里面管这个特性叫preset & clear,才恍然大悟查错了资料。后来换了个方式查找资料,果然搜到了。
- 异步复位的D锁存器设计
- 异步设置D锁存器设计
- 异步复位的D触发器设计
- 异步设置D触发器设计
3.8.4 时序逻辑电路的设计:从状态机到电路(尤其是Mealy型电路的设计)
Moore型电路和Mealy型电路的主要差别在于:Moore型电路的输出与状态有关,而Mealy型电路的输出与状态和输入有关。
Mealy型电路的设计还不太会(如课本P166 习题3.25)(说白了其实是DFA的设计不太会,过会儿补一补) DFA的介绍看这里:
3.8.4.1 状态机的化简流程
状态机的化简看这里:
化简流程:
- 根据状态转换图,画出状态转换表
- 消去等效状态
- 把表中消去的等效状态用已有的状态替代
- 画出新的状态转换图
3.8.4.2 二进制序列检测器
基础二进制序列检测器的实现方法看这里:
3.8.4.3 Grey Code状态机生成器
3.8.5 时序逻辑电路的分析:从电路到状态机
3.8.6 时序逻辑电路中的限制与延迟
3.9 Interview Questions
4 Chapter 4:硬件描述语言
这一章的学习可以配套 HDLBits 的 Verilog 练习,以及其他学校的 Verilog 数字电路设计课程进行练习,光看是没有用的。
5 Chapter 5:数字电路设计
这一章的学习过程中,可以使用 Logisim 将所有基础电路搭起来,并且使用 Verilog 构建所有的电路
6 Chapter 6:RISC-V 汇编语言
这一章学习过后可以学习汇编和链接过程,文件格式,实现一个 RISC-V 汇编器,和一个 RISC-V 反汇编器
7 Chapter 7:微架构处理器设计
这一章学习后,可以使用 Logisim 实现 MIPS 单周期/多周期/流水线处理器(完成华科头歌实验),并用 Verilog 进行实现并仿真
8 Chapter 8:主存和 I/O 系统设计
这一章学习后,可以使用 Logisim 实现简单的 Memory 和 Cache(完成华科头歌实验),而后可以使用 Verilog 实现并仿真
9 后续任务
- 华科数字逻辑+组成原理课程学完
- 其他学校数字逻辑+组成原理课程学完
- Verilog 基础数字电路构建块设计
- 设计一些小型的数字电路
- 实现一个带存储+I/O+五级流水的 MIPS CPU
- 文件格式学习
- 链接过程学习
- MIPS 汇编器实现
- MIPS 反汇编器实现
- 学习基础的编译原理知识
- 小型 C 语言编译器实现